Złożoność obliczeniowa i jej wyrażanie

Wstęp

Jako front-end developerzy, z reguły skupiamy się na jak najszybszym rozwiązaniu danego problemu, nie przywiązując zbyt dużej uwagi do wydajności naszego kodu. Najczęściej pracujemy nad stronami internetowymi, gdzie to backend ma najwięcej pracy, jeśli chodzi o logikę biznesową. Zdarza się jednak czasami, że stajemy przed problemem wymagającym skomplikowanego algorytmu. W takich sytuacjach powinniśmy spojrzeć szerzej i zastanowić się, czy aby na pewno rozwiązanie, które stworzyliśmy, jest szybkie, czy zajmuje tyle pamięci, ile jest konieczne, i jak się zachowa przy dużo większej ilości danych. Jak to zrobić? Z użyciem złożoności obliczeniowej

Po co oceniać złożoność obliczeniową?

Załóżmy, że mamy dwa algorytmy wykonujące dokładnie te samą czynność. Jednakże, każdy z nich dochodzi do wyniku na swój sposób. Jeden korzysta ze wzoru matematycznego, a drugi wykorzystuje nowatorskie podejście do tematu. Czy oba wykorzystująć zasoby komputera w ten sam sposób? Czy czas wykonania będzie taki sam? Jak sprawdzić, który z nich jest lepszy? Ten, który został napisany przez bardziej doświadczonego programistę? A może ten, który wykorzystuje techniki algorytmiczne znane od dziesięcioleci? Trzeba to sprawdzić w sposób mierzalny, który jednoznacznie określa przewagę jednego rozwiązania na drugim. Właśnie tutaj wkracza ocenianie złożoności obliczeniowej.

Co to jest ta złożoność obliczeniowa?

W skrócie, jest to miara, pozwalająca na jednoznaczne określenie jak „dobry” jest dany algorytm zależnie od ilości wprowadzonych do niego danych. Można ją podzielić na dwie kategorie – złożoność czasową (time complexity) i złożoność pamięciową (space complexity). Pierwsza określa jak dużo czasu, zależnie od ilości danych wejściowych, zajmie jedno przejście algorytmu. Druga, ile pamięci zostanie zalokowane w trakcie wykonywania obliczeń.

Czego używamy do określenia złożoności

Stosujemy do tego notację dużego O (big O notation). Ma ona postać O(f(n)), gdzie f(n) to funkcja, która określa asymptotę krzywej złożoności czasowej danego algorytmu. Asymptota, to taka prosta, do której wraz ze zbliżaniem się wartości na osi x do nieskończoności, zbliża się dana krzywa. Żeby łatwiej to sobie wyobrazić, zastosujemy analogię. Wyobraźmy sobie próbę zrozumienia płci przeciwnej. Wraz z wiekiem, rośnie nasze pojmowanie przeciwnego gatunku ludzkiego, jednak nigdy nie osiąga ono 100%. Wyrażając 100% jako 1, czyli całkowite zrozumienie (u), wiemy, że nigdy nie osiągniemy tej wartości, jednakże dążymy do niej całe życie. W ten sposób, przy czasie (t) dążącym do nieskończoności, możemy wykreślić krzywą naszego zrozumienia (cu) zależną od czasu. Przedstawia to poniższy wykres.

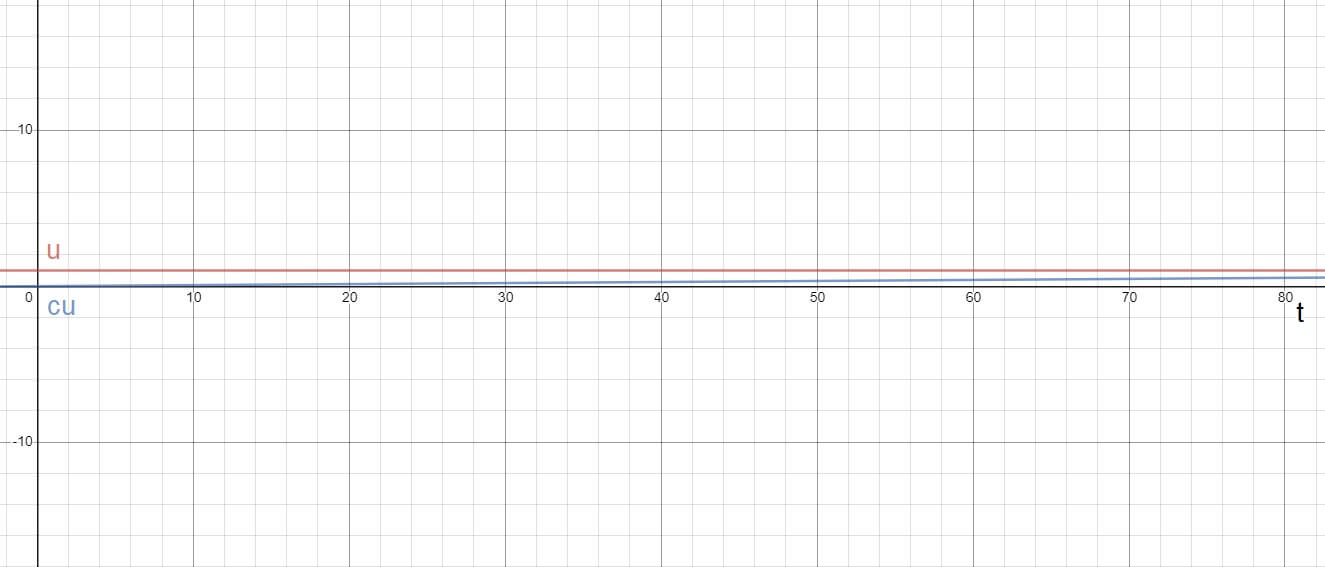
Jak widać, nasze zrozumienie (cu) zbliża się wraz z wiekiem (t) do całkowitego zrozumienia (u), ale nigdy go nie osiąga. Wychodząc z analogii, zrozumienie (cu) to wykres czasu potrzebnego na wykonanie algorytmu, wiek (t) to ilość danych wejściowych, a całkowite zrozumienie (u) to nasza asymptota, czyli złożoność obliczeniowa.

Trochę prostszymi słowy

Mamy kilka kluczowych funkcji, które najczęściej określają złożoność obliczeniową. Są to przede wszystkim: 1, log(n), n, nlog(n), n², gdzie n to ilość danych wejściowych. Zapisane przy użyciu notacji dużego O wyglądałyby w następujący sposób O(1), O(log(n)), O(n), O(nlog(n)), O(n²). Im większa wartość funkcji po podstawieniu przykładowej liczby za n, tym większa jest złożoność czasowa algorytmu i tym gorszy jest ten algorytm.

• O(1) – oznacza stałą liczbę operacji, niezależnie od ilości danych wejściowych, cel
• O(log(n)) – oznacza logarytmiczną zależność, bdb
• O(n) – oznacza liniową zależność, db
• O(n²⁾ – oznacza zależność kwadratową, dst
• i tak dalej

Dlaczego powinienem się tym przejmować?

Najłatwiej zobrazować to przykładem. Szef zlecił Ci projekt, w którym jednym z wymagań jest zliczanie sumy wszystkich liczb do podanej liczby. Pierwsze, co przyszło Ci do głowy, to zrobienie pętli i dodawanie każdej kolejnej liczby do sumy. Teoretycznie wykonałeś zadanie, ale można to zrobić lepiej. Istnieje wzór matematyczny na obliczanie takiej sumy. Jeśli napiszesz ten sam algorytm z jego wykorzystaniem, to ilość operacji wyniesi 3, niezależnie od wielkości n. Twój oryginalny algorytm miał złożoność O(n), a ten wykorzystujący wzór O(1). W ten sposób, przy sumowaniu miliona liczb, oszczędzasz praktycznie milion operacji. Widzisz już potencjał?

Obliczanie złożoności obliczeniowej

Obliczając złożoność obliczeniową, patrzymy na ilość operacji.

function example(n) {
	const halfN = n / 2; // 1 operacja
	
	for (let i = 0; i < n; i++) { // n operacji
		console.log(i) // 1 operacja na każde n
	}
	
	console.log(halfN); // 1 operacja
	halfN++; // 1 operacja
}

W powyższym przykładzie mamy 13 operacji dla n = 5, 23 operacje dla n = 10. Można z tego wywnioskować, że wykonujemy 2n + 3 operacji. Jednakże nie jest to nasza złożoność algorytmiczna. Powyższy wynik upraszczamy, pozbywając się stałych (tutaj 3) i wielokrotności n (tutaj 2). Pozostaje nam n, które jest naszą funkcją złożoności algorytmicznej, dając nam złożoność O(n).

Zasady obliczania złożoności

1. Jeśli pętla występuje w pętli, to ich złożoności są mnożone.
2. Jeśli pętla następuje po pętli, ich złożoności są dodawane.
3. Praktycznie każda pętla zależna od n ma złożoność n razy ilość operacji – O(n)
4. Operacje arytmetyczne mają stałą złożoność – O(1)
5. Przypisania do zmiennych mają stałą złożoność – O(1)
6. Odczytywanie tablic komórek i właściwości obiektów mają stałą złożoność – O(1)

Przykłady algorytmów o różnej złożoności

Przeanalizuj poniższe przykłady z pomocą powyższych zasad obliczania złożoności. Pozwoli Ci to zrozumieć, dlaczego algorytm ma taką, a nie inną złożoność. Powinieneś, przede wszystkim, zwrócić uwagę na ilość pętli i ich relację wobec siebie.

// Suma kolejnych liczb naturalnych
//
// O(1)

function sumRange(n) {
	return (n * (n + 1)) / 2;
}

// Wyszukiwanie binarne
//
// O(log(n))

function binarySearch(arr, value) {
	let low = 0;
	let high = arr.length -1;
	let mid;     
	
	while (low <= high) {
	  mid = Math.floor((low + high) / 2);

		if (arr[mid] === value) {
		  return mid;
		} else if (arr[mid] < value) {
		  low = mid + 1;
		} else {
		  high = mid - 1;
		}
	}
	
	return -1 ;
}

// Wyszukiwanie liniowe (kopia Array.indexOf())
//
// O(n)

function linearSearch(arr, elToFind) {
  for (var i = 0; i < arr.length; i++) {
    if (arr[i] === elToFind) {
      return i;
    }
  } return -1;
}

// Sortowanie bąbelkowe
//
// O(n^2)

function bubbleSort(arr) {
	const length = arr.length;
    
	for (var i = 0; i < length ; i++) {
		for(var j = 0 ; j < length - i - 1; j++){
			if (arr[j] > arr[j + 1]) {
				var temp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = temp;
			}
		}
	}
	
	return arr;
}

Podsumowanie

Złożoność obliczeniowa nie jest skomplikowanym zagadnieniem, ale niestety wiele osób, przede wszystkim początkujących, nie wie o jego istnieniu. Nie trzeba dużo czasu by pojąć „o co kaman”, a można wiele zyskać – zarówno w oczach klienta, jak i szefa i współpracowników. Bez problemu można przyspieszyć wykonywanie operacji na dużej ilości danych, niejednokrotnie ucinając czas wykonania algorytmu o ponad połowę. Jest to niezbędna wiedza dla osoby, która myśli o programowaniu na poważnie.